Численные методы решения уравнений в среде MatLab

В этом посте я расскажу о численных методах решения уравнений, что очень удобно для их расчёта на компьютере. Приведу 3 вида и 3 примера кода, для каждого вида соответственно, а также расскажу о предостерегающих трудностях и путях их решения.

Иногда нам приходится решать уравнения, кому-то по работе, а кому-то понадобилась для домашних нужд — назовём это так. В школе нас учили, что для решения уравнения, необходимо выразить искомую переменную и тогда мы получим символьное решение уравнения, а если вместо букв поставить числа, то получим численное решение того или иного уравнения. Однако, бывают такие уравнения, в которых нельзя явно выразить искомую переменную, например, уравнение ниже.

sin(x)tg(x)ln(x)=4

Решать такие уравнения приходиться численно, то есть получая ответ в виде числа, а если вам нужна зависимость, то придётся задать диапазон начальных условий и получить, соответственно, диапазон значений искомого параметра.

Предлагаю вам ознакомиться с моей презентацией, а после чего прочитать комментарии и пояснения к ней ниже. Также, в конце записи я опубликовал листинги программ для расчёта указанными методами в среде MatLab.

При решении уравнений 2 или 3 типа, может возникнуть ситуация , когда из большого шага между двумя значениями x и(или) y, мы можем не достичь требуемой точности и тогда результат будет не предсказуем. Для избежания таких случаев предлагаю использовать не сравнение результата с заданным уровнем точности, а сравнение точностей для каждого значения переменной и выбор значения с наибольшей точностью. Подробнее  расскажу на примере кода. Рекомендую использовать следующей алгоритм действий для уравнений типа f(x)=const:

1. разбиваете заданный диапазон значений на n равных интервалов и получаете n+1 значений x
2. решаете уравнение для каждого значения х
3. выбираете то значение х_i, при котором точность максимальна.
4. из п. 3 следует, что точное решение находится между х_i-1 и х_i+1. Устанавливаете новый диапазон значений для x от х_i-1 до х_i+1 , сохраняя то же число интервалов.
5. Вновь расчитываете уравнение для нового интервала с новым шагом
6. Повторяете указанные действия до тех пор, пока интервал значений х не будет достаточно мал, чтобы получить требуемую точность вычислений.

Аналогичный алгоритм, лишь с некоторым поправками, можно использовать и для решения уравнений вида f(x,y)=y.

Если кому интересно, то ниже производится решение следующего уравнения относительно γ.

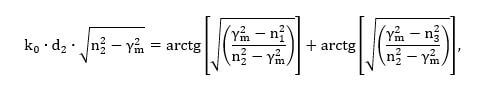
% Задаём исходные данные
lamda=632.8*10^-9; % Длина волны излучения
k0=2*pi/lamda; % Расчитвыаем волновое число
d2=1*10^-6; % Толщина волноводного слоя
n1=1.335; % Показатель преломления чистого полимера
n2=1.7476; % Показатель преломления подложки CTK19
n3=1; % Показатель преломления среды - воздух

eps=10^-6; % Задаём точность
gamma_cp=1.3; % Задаём приближённое значение
razn=1; % Задаём начальное значение разности x(i+1)-x(i). Значение должно быть заведомо больше eps.
i=0; % Зададим начальное значение счётчика итераций.
% Зададим уравнение как функцию g(d2,gamma_cp,k0,n1,n2,n3), где все аргументы, кроме gamma_cp являются константами, т.е. по сути g(gamma_cp)=gammka_cp.
g=inline('sqrt(n2^2-((atan(sqrt((gamma_m^2-n1^2)/(n2^2-gamma_m^2)))+atan(sqrt((gamma_m^2-n3^2)/(n2^2-gamma_m^2))))/(k0*d2))^2)');
// начинаем циклический подсчёт
while(razn>eps) { % выполняем цикл пока не достигнем требуемой точности
    i=i+1; % увеличиваем на единицу количество выполненых итераций
    gamma_temp=g(d2,gamma_cp,k0,n1,n2,n3); % расчитываем итерацию
    razn=abs(gamma_temp-gamma_cp); % расчитываем погрешность
    gamma_cp=gamma_temp; % Устанавливаем результат данной итерации как приближённое значение искомой переменной gamma_cp
}
gamma_cp % Выводим на экран результат вычислений
i % Выводим на экран количество пройденых итераций

Этот код решает следующее уравнение относительно θ.

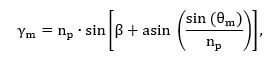
gamma=[1:0.0001:1.33]; % Задаём диапазон значений гаммы
for i=[1:length(gamma)] % Выполняем тело цикла для каждого значения гаммы от первого до последнего
	% Задаём вспомогательные и служебные переменные
	razn=100;
	tetz=0;
	raz=100;
	run=1;
	teta_n=61.6*pi/180; % Задаём начальное значение угла (определено приближениями)
	% Высчитываем значение с точностью до 1/10 угловой секунды
	while(run)
		teta_n=teta_n+pi/(180*60*60*10);
		razn=abs(gamma(i)-np*sin(beta+asin(sin(teta_n)/np)));
		% Если текущее значение имеет более высокую точность, чем предыдущее, то записываем это значение и его погрешность.
		if razn<raz
			tetz=teta_n;
			raz=razn; 
		end
		% Прерываем расчёт при угле больше 61,7 градусов, т.к. за пределами указанного диапазона (61.6-61.7) решений нет
		if teta_n>=(61.7*pi/180)
			run=0;
		end
	end
	teta_m(i)=tetz*180/pi; % Переводим результат в градусы и записываем в массив ответов
end

На выходе данной программы получаем массив значений угла θ. Границы диапазона θ от 61.7 до 61.8 найдены путём последовательных приближений. Сначала уравнение решалось для всех гамма в пределах угла от 1 до 90 с шагом в 1 градус, затем диапазон сужался по тому же принципу, что и в случае с предыдущем кодом, и действия повторялись до достижения требуемой точности.

Если у вас есть какие-либо вопросы, замечания или предложения, то их в комментариях к данному посту! Удачных вам математических расчётов!