Статья посвящена таблицам Карно, которые широко используются в программировании и логике для создания или упрощения логических функций, состоящих из многих аргументов.
Сейчас июнь, сессия в самом разгаре, но так вышло (парадокс), что в сессию у меня больше свободного времени, чем в течении учебного года, поэтому во время сессий и каникул в моём блоге можно наблюдать наибольшую активность. Что-же поделать? Нравиться мне учиться и всё. Для тех кто не знает или ещё не понял — речь пойдёт о программировании и логике, а не о продаже квартир в Ядрине. ![]()
Таблица Карно представляет собой, по сути, таблицу истинности, но немного видоизменённую. Подробнее и понятнее расскажу позже на примере. Таблицы Карно, их ещё иногда называют картами Карно, используют для упрощения или составления логических функций, зная возможные значения переменных и зная значение функции при заданных значениях переменных. Это может быть полезно как при разработке логических схем, так и в программировании, например, мне пришлось прибегнуть к использованию таблицы Карно при составлении условия выполнения цикла while при написании программы. В итоге я хохотал, получив в результате простую базовую функцию логическое-И, но сейчас не об этом. Существует 7 правил построения указанной таблицы:
- Количество клеток таблицы равно количеству строк таблицы истинности
- Слева и сверху располагаются значения аргументов. При этом, в двух соседних по горизонтали и вертикали клетках отличается значение только одного аргумента. Отсюда следует, что клетки находящиеся на противоположных концах таблицы тоже являются соседними.
- В клетки заносятся соответствующие значения логической функции
- Клетки, где функция равна единице, объединяются в импликанты (прямоугольники) по 2n клеток. Импликанты могут перекрываться друг с другом. Желательно, составлять импликанты как можно большего размера.
- Для каждого импликанта записывается произведение тех аргументов, которые не изменяют своего значения в соседних клетках, для всего рассматриваемого импликанта.
- Переменные входят в произведение в прямом виде, если их значение равно единице и в инверсном, если нулю.
- Полученные произведения складываются по ИЛИ в искомую логическую функцию
Есть непонятности? Сейчас разберём на примере и точно поймёте.
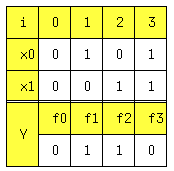
Таблица истинности для функции “исключающее ИЛИ” (XOR)
Рассмотрим пример функции исключающее-или. Эта функция равна единице только тогда, когда составляющие её переменные не равны между собой. Для простоты рассмотрим случай для двух переменных и составим соответствующую таблицу Карно, которая будет выглядеть как указано выше. Составив таблицу мы выполнили первые 3 шага. Теперь необходим объединить в импликанты ячейки с единицами или с нулями (в таком случае мы найдём инверсное значение логической функции). Я рассмотрю пример с единицами, а случай с нахождением инверсной логической функции оставлю вам потренироваться. Для правой верхней единицы мы можем записать следующее логическое произведение аргументов ~x2x1 (~ – это инверсия), т. к. в нашем случае ни одна из переменных не изменяет своего значения в пределах выбранного импликанта, но переменная x2 входит в произведение в инверсном виде, поскольку её значение, в данном случае, равно нулю. Для левой нижней единицы получим произведение x2~x1. Таким образом, искомая логическая функция выглядит следующим образом Y=~x2x1+x2~x1.
Используя теорему двойственности, которая утверждает, что инверсия произведения равно сумме произведений, и наоборот, инверсия суммы равна инверсии произведений (см. формулу ниже), выведите ту же самую функцию исключащего-или, но через импликанты нулевых ячеек.
![]()
![]()
Законы Де Моргана
Если у вас остались вопросы или что-то не ясно, то пишите ваши вопросы, предложения и пожелания в комментариях к этому посту.
